跳到主要内容

[TOC]

实现神经网络模型的一般流程

  1. 准备数据
  2. 定义模型
  3. 训练模型
  4. 评估模型
  5. 使用模型
  6. 保存模型

pytorch 动态计算图

https://mp.weixin.qq.com/s/XpcgV5vDlEJ3HqhQwJ_vxw

Pytorch 中的计算图是动态图。这里的动态主要有两重含义。

第一层含义是：计算图的正向传播是立即执行的。无需等待完整的计算图创建完毕，每条语句都会在计算图中动态添加节点和边，并立即执行正向传播得到计算结果。

第二层含义是：计算图在反向传播后立即销毁。下次调用需要重新构建计算图。如果在程序中使用了 backward 方法执行了反向传播，或者利用 torch.autograd.grad 方法计算了梯度，那么创建的计算图会被立即销毁，释放存储空间，下次调用需要重新创建。

2022-8-1

DGMR 中 loss 采用 SSIM(Structural Similarity) ，结构相似性，是一种衡量两幅图像相似度的指标。比 MSEloss 收敛更快。pytorch 实现：pytorch-msssim

2022-8-22

batch_size 的作用

a

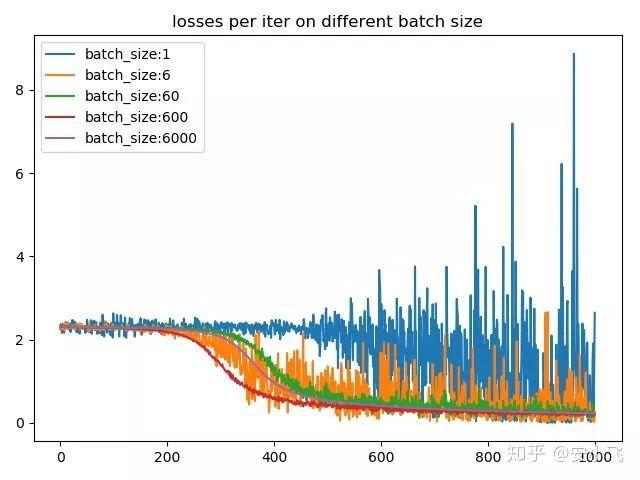
深度学习 | Batch Size 对训练的影响（二） - 知乎 (zhihu.com)

batch_size 也可以提高 GPU 的利用率。 一般而言，batch_size 不影响随机梯度的期望，但是会影响随机梯度的方差。 batch_size 越大，随机梯度的方差越少，引入的噪声越少，训练也越稳定，因此可以设置较大的学习率 ，反之亦然。

学习率预热

在小批量梯度下降法中，当批量大小设置比较大时，通常需要比较大的学习率，但在刚开始训练的时，由于参数是随机初始化的，梯度往往也比较大，加上比较大大初始学习率，会使训练变得不稳定。 为了提高训练稳定性，可以在最初的几轮迭代中，采用较小的学习率，等到梯度下降到一定程度后再恢复到初始的学习率，这种方法称为学习率预热（Learning Rate Warmup）。 一个常用的学习率的预热的方法是逐渐预热（Gradual Warmup）。假设预热的迭代次数为 T‘T^‘ 初始学习率为 α0\alpha_0 , 在预热的过程中每次更新的学习率为：

αt‘=tT‘α0   1≤t≤T‘ \alpha^‘_t =\frac{t}{T^‘}\alpha_0 \ \ \ 1 \leq t \leq T^‘

当预热过程结束，再选择一种学习率衰减的方法来逐渐降低学习率

梯度截断

在深度神经网络或循环神经网络中，除了梯度消失之外，梯度爆炸也是影响学习效率的主要因素。在基于梯度下降的优化过程中，如果梯度突然增大，用大的梯度更新参数反而会导致器远离最优点。为了避免这种情况，当梯度的模大于一定阈值的时候会，就对梯度进行截断，称为梯度截断

参数初始化

深度神经网络的参数学习是一个非凸优化问题。当使用梯度下降的来进行有优化网络参数的时，参数初始值的选取十分关键，关系到网络的优化效率和泛化能力。参数初始化的方式有以下三种：

  1. 预训练初始化 ：不同的参数初始值会收敛到不同的局部最优解。虽然这些局部最优解在训练集哈桑的损失比较接近，但是他们的泛化能力差异很大。一个好的初始值会使得网络收敛到一个泛化能力比较高的局部最优解。通常情况下，一个已经在大规模数据上训练过的模型可以提供一个好的参数初始化值，这种初始化方法称为预训练初始化 。预训练任务可以为监督学习和无监督学习任务。
  2. 随机初始化 ：咋线性模型的训练（比如感知机和 Logistic 回归）中，一般将参数全部初始化为 0，但是在神经网络的训练中会存在一些问题，因为如果参数为 0 .在第一遍前向计算的过程中，所有的隐层神经元没有区分性。这种现象也称为 对称权重 现象。为了避免这种现象，比较好的方式就是对每个参数进行随机初始化（Random Initialization） ，这样使得不同神经元之间的区分性更好。
  3. 固定值初始化 ：对于一些特殊的参数，我们可以根据经验用一个特殊的固定值来进行初始化。比如偏置（Bias）通常用 0 来初始化，但是有时可以设置某些经验值来提高优化效率，在 LSTM 网络的遗忘门中，偏置通常初始化为 1 和 2，使得时序上的梯度比较大，对于使用 ReLU 的神经元，有时也可以将偏置设置为 0.01，使得 ReLU 神经元在训练初期更容易激活从而获得一定的梯度来进行误差的反向传播。

逐层归一化

在深度神经网络中，中间某一层的输入是其之前的神经层的输出。因此，其之前的神经层的参数变化会导致其输入的分布发生较大的差异，在使用随机梯度下降来训练网络时，每次参数更新都会导致网络中间的每一层的输入的分布发生改变，越深的层，其输入的分布会改变的越明显，就先一栋高楼，低楼层发生的一个较小的偏移，都会导致高楼层发生较大的偏移。 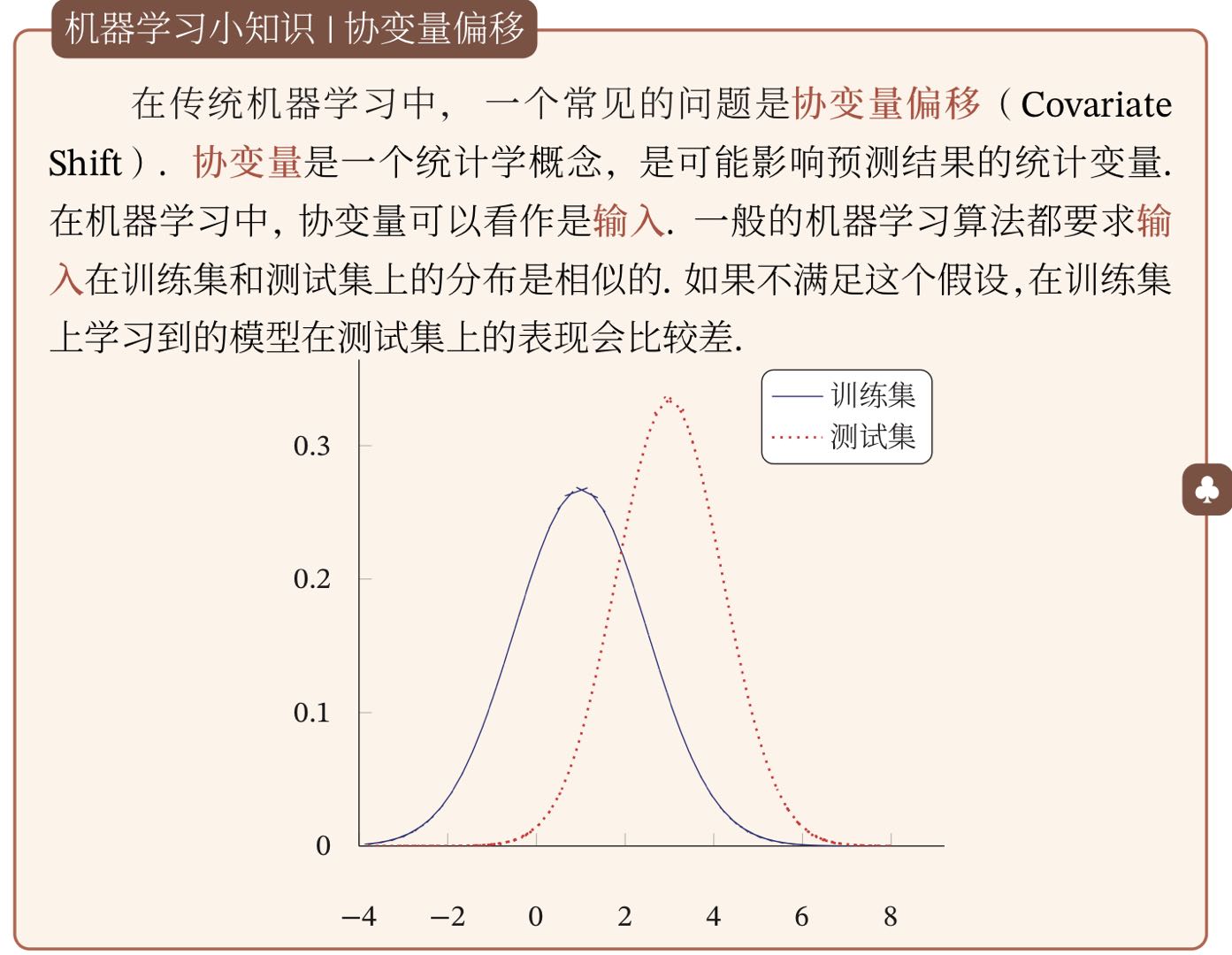协变量的迁移 为了解决内部协变量偏移的问题，就要使得每一个神经层的输入的发呢不在训练过程中保持一致。最简单直接的方法就是对每一个神经吃呢都进行归一化操作，使得其分布保持稳定。几种比较常用的逐层归一化方法：批量归一化，层归一化和其他一些方法。

  1. 批量归一化（Batch Normalization,BN） 方法是一种有效的逐层归一化方法，可以对神经网络中的任意的中间层进行归一化操作。 对于一个深度神经网络，令第 l 层的的净输入为 ZlZ^l ，神经元的输出为 ala^l 即
al=f(zl)=f(Wal−1+b) a^l=f(z^l) =f(Wa^{l-1}+b)

其中 f(⋅)f(·) 是激活函数，W 和 b 是可学习的参数。 为了减少内部协变量偏移问题，就要使得净输入 ZlZ^l 的分布一致，比如都归一化到标准正态分布。虽然归一化操作可以应用在输入的 a(l−1)a^{(l-1)} 上，但其分布性质不如 ZlZ^l 稳定。因此，在实践中归一化操作一般应用在仿射变换之后，激活函数之前。 批量归一化操作可以看作是一个特殊的神经层，加在每一层的非线性激活函数之前。

  1. 层归一化（Layer Normalization） 是和批归一化非常类似的方法。层归一化是对一个中间的所有神经元进行归一化， 对于一个深度神经网络，令第 l 层神经元的净输入为 zlz^l 其均值和方差为： μl=1Ml∑i=1Mlzil,\mu^l=\frac{1}{ M_l } \sum_{i=1}^{ M_l }z_i^l ,
σl2=1Ml∑i=1Ml(zil−μl)2\sigma^{l^2}=\frac{1}{ M_l }\sum_{i=1}^{ M_l }(z^l_i-\mu^l)^2

其中 MlM_l 为第 l 层的神经元的数量。 层归一化定义为：

​aaas1

​

其中 γ\gamma 和 β\beta 分别代表缩放和平移的参数向量，和 zlz^l 维数相同。

循环神经网络的层归一化 层归一化可以应用在循环网络中，对循环神经层进行归一化操作，假设在时刻 t，循环神经网络的隐藏层为 hth_t ，其层归一化的的更新为：

zt=Uht−1+Wxt,z_t=Uh_{t-1}+ Wx_t,

其中输入为 xtx_t 为第 t 时刻的输入，U 和 W 为网络参数。 循环神经网络的层归一化，可以有效缓解梯度爆炸或消失。

网络正则化

机器学习模型的关键是泛化问题，即在样本真实分布上的期望风险最小化，而训练数据集上的经验风险最小化和期望风险并不一致。 正则化（Regularization） 是一类通过限制模型复杂度，从而避免过拟合，提高泛化能力的方法，比引入约束、增加先验，提前停止等等。

Dropout 正则化： 指在深度学习网络的过程中，对于神经网络单元，按照一定的概率将其暂时从网络中丢弃。注意是暂时，对于随机梯度下降来说，由于是随机丢弃，故而每一个 mini-batch 都在训练不同的网络。

drop

代码实现（pytorch）： nn.Dropout(p,arg)

p 是被舍弃的概率失活的概率

循环神经网络上的丢弃法 ： 当在循环神经网络上应用丢弃法时，不能直接对每个时刻的隐状态进行随机丢弃这样会损坏循环网络在时间维度上的记忆能力，一种简单的方法是对非时间维度的连接（即非循环的连接）进行随机丢失。

Pytorch torch.optim 优化器

Pytorch 官网教程 optim 优化 — PyTorch 1.12 文档

 torch.optim.SGD([
                {'params': model.base.parameters()},
                {'params': model.classifier.parameters(), 'lr': 1e-3}
            ], lr=1e-2, momentum=0.9)
# 这样 base 的参数的学习率为 1e-2，而 classifier 的参数的学习率 1e-3
# 一般的计算梯度，更新参数的普通方法
optimizer.zero_grad()  # 梯度清零
output=model(inputx)
loss=loss_function(output,y)
loss.backward() # 反向传播
optimizer.step() # 梯度更新

循环训练代码示例

epochs = 10
log_step_freq = 30

dfhistory = pd.DataFrame(columns = ["epoch","loss",metric_name,"val_loss","val_"+metric_name]) 
print("Start Training...")
nowtime = datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S')
print("=========="*8 + "%s"%nowtime)

for epoch in range(1,epochs+1):  

    # 1，训练循环-------------------------------------------------
    net.train()
    loss_sum = 0.0
    metric_sum = 0.0
    step = 1
    
    for step, (features,labels) in enumerate(dl_train, 1):
    
        # 梯度清零
        optimizer.zero_grad()

        # 正向传播求损失
        predictions = net(features)
        loss = loss_func(predictions,labels)
        metric = metric_func(predictions,labels)
        
        # 反向传播求梯度
        loss.backward()
        optimizer.step()

        # 打印 batch 级别日志
        loss_sum += loss.item()
        metric_sum += metric.item()
        if step%log_step_freq == 0:   
            print(("[step = %d] loss: %.3f, "+metric_name+": %.3f") %
                  (step, loss_sum/step, metric_sum/step))
            
    # 2，验证循环-------------------------------------------------
    net.eval()
    val_loss_sum = 0.0
    val_metric_sum = 0.0
    val_step = 1

    for val_step, (features,labels) in enumerate(dl_valid, 1):
        
        predictions = net(features)
        val_loss = loss_func(predictions,labels)
        val_metric = metric_func(predictions,labels)

        val_loss_sum += val_loss.item()
        val_metric_sum += val_metric.item()

    # 3，记录日志-------------------------------------------------
    info = (epoch, loss_sum/step, metric_sum/step, 
            val_loss_sum/val_step, val_metric_sum/val_step)
    dfhistory.loc[epoch-1] = info
    
    # 打印 epoch 级别日志
    print(("\nEPOCH = %d, loss = %.3f,"+ metric_name + \
          "  = %.3f, val_loss = %.3f, "+"val_"+ metric_name+" = %.3f") 
          %info)
    nowtime = datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S')
    print("\n"+"=========="*8 + "%s"%nowtime)
        
print('Finished Training...')

函数形式训练循环

import pandas as pd 
from sklearn.metrics import roc_auc_score

model = net
model.optimizer = torch.optim.SGD(model.parameters(),lr = 0.01) # 设置优化器
model.loss_func = torch.nn.BCELoss()
model.metric_func = lambda y_pred,y_true: roc_auc_score(y_true.data.numpy(),y_pred.data.numpy())
model.metric_name = "auc"
def train_step(model,features,labels):
    
    # 训练模式，dropout 层发生作用
    model.train()
    
    # 梯度清零
    model.optimizer.zero_grad()
    
    # 正向传播求损失
    predictions = model(features)
    loss = model.loss_func(predictions,labels)
    metric = model.metric_func(predictions,labels)

    # 反向传播求梯度
    loss.backward()
    model.optimizer.step()

    return loss.item(),metric.item()

def valid_step(model,features,labels):
    
    # 预测模式，dropout 层不发生作用
    model.eval()
    
    predictions = model(features)
    loss = model.loss_func(predictions,labels)
    metric = model.metric_func(predictions,labels)
    
    return loss.item(), metric.item()


# 测试 train_step 效果
features,labels = next(iter(dl_train))
train_step(model,features,labels)
def train_model(model,epochs,dl_train,dl_valid,log_step_freq):

    metric_name = model.metric_name
    dfhistory = pd.DataFrame(columns = ["epoch","loss",metric_name,"val_loss","val_"+metric_name]) 
    print("Start Training...")
    nowtime = datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S')
    print("=========="*8 + "%s"%nowtime)

    for epoch in range(1,epochs+1):  

        # 1，训练循环-------------------------------------------------
        loss_sum = 0.0
        metric_sum = 0.0
        step = 1

        for step, (features,labels) in enumerate(dl_train, 1):

            loss,metric = train_step(model,features,labels)

            # 打印 batch 级别日志
            loss_sum += loss
            metric_sum += metric
            if step%log_step_freq == 0:   
                print(("[step = %d] loss: %.3f, "+metric_name+": %.3f") %
                      (step, loss_sum/step, metric_sum/step))

        # 2，验证循环-------------------------------------------------
        val_loss_sum = 0.0
        val_metric_sum = 0.0
        val_step = 1

        for val_step, (features,labels) in enumerate(dl_valid, 1):

            val_loss,val_metric = valid_step(model,features,labels)

            val_loss_sum += val_loss
            val_metric_sum += val_metric

        # 3，记录日志-------------------------------------------------
        info = (epoch, loss_sum/step, metric_sum/step, 
                val_loss_sum/val_step, val_metric_sum/val_step)
        dfhistory.loc[epoch-1] = info

        # 打印 epoch 级别日志
        print(("\nEPOCH = %d, loss = %.3f,"+ metric_name + \
              "  = %.3f, val_loss = %.3f, "+"val_"+ metric_name+" = %.3f") 
              %info)
        nowtime = datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S')
        print("\n"+"=========="*8 + "%s"%nowtime)

    print('Finished Training...')
    
    return dfhistory

epochs = 20

dfhistory = train_model(model,epochs,dl_train,dl_valid,log_step_freq = 50)

打印模型结构

import torchkeras
torchkeras.summary(net,input_shape= (3,32,32))

输出

----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
            Conv2d-1           [-1, 32, 30, 30]             896
         MaxPool2d-2           [-1, 32, 15, 15]               0
            Conv2d-3           [-1, 64, 11, 11]          51,264
         MaxPool2d-4             [-1, 64, 5, 5]               0
         Dropout2d-5             [-1, 64, 5, 5]               0
 AdaptiveMaxPool2d-6             [-1, 64, 1, 1]               0
           Flatten-7                   [-1, 64]               0
            Linear-8                   [-1, 32]           2,080
              ReLU-9                   [-1, 32]               0
           Linear-10                    [-1, 1]              33
          Sigmoid-11                    [-1, 1]               0
================================================================
Total params: 54,273
Trainable params: 54,273
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.011719
Forward/backward pass size (MB): 0.359634
Params size (MB): 0.207035
Estimated Total Size (MB): 0.578388
----------------------------------------------------------------

能够输出网络结构，参数个数，大小。

模型层

pytorch 不区分模型和模型层，都是通过继承 nn.Module 进行构建。因此，我们只要继承 nn.Module 基类并实现 forward 方法即可自定义模型层。

基础层​

  • nn.Linear：全连接层。参数个数 = 输入层特征数× 输出层特征数 (weight)＋ 输出层特征数 (bias)

  • nn.Flatten：压平层，用于将多维张量样本压成一维张量样本。

  • nn.BatchNorm1d：一维批标准化层。通过线性变换将输入批次缩放平移到稳定的均值和标准差。可以增强模型对输入不同分布的适应性，加快模型训练速度，有轻微正则化效果。一般在激活函数之前使用。可以用 afine 参数设置该层是否含有可以训练的参数。

  • nn.BatchNorm2d：二维批标准化层。

  • nn.BatchNorm3d：三维批标准化层。

  • nn.Dropout：一维随机丢弃层。一种正则化手段。

  • nn.Dropout2d：二维随机丢弃层。

  • nn.Dropout3d：三维随机丢弃层。

  • nn.Threshold：限幅层。当输入大于或小于阈值范围时，截断之。

  • nn.ConstantPad2d：二维常数填充层。对二维张量样本填充常数扩展长度。

  • nn.ReplicationPad1d：一维复制填充层。对一维张量样本通过复制边缘值填充扩展长度。

  • nn.ZeroPad2d：二维零值填充层。对二维张量样本在边缘填充 0 值。

  • nn.GroupNorm ：组归一化。一种替代批归一化的方法，将通道分成若干组进行归一。不受 batch 大小限制，据称性能和效果都优于 BatchNorm 。

    归一化参考文章 https://zhuanlan.zhihu.com/p/34858971

  • nn.LayerNorm：层归一化。较少使用。

  • nn.InstanceNorm2d : 样本归一化。较少使用。

卷积网络相关层​

  • nn.Conv1d：普通一维卷积，常用于文本。参数个数 = 输入通道数×卷积核尺寸 (如 3)×卷积核个数 + 卷积核尺寸 (如 3）
  • nn.Conv2d：普通二维卷积，常用于图像。参数个数 = 输入通道数×卷积核尺寸 (如 3 乘 3)×卷积核个数 + 卷积核尺寸 (如 3 乘 3) 通过调整 dilation 参数大于 1，可以变成空洞卷积，增大卷积核感受野。通过调整 groups 参数不为 1，可以变成分组卷积。分组卷积中不同分组使用相同的卷积核，显著减少参数数量。当 groups 参数等于通道数时，相当于 tensorflow 中的二维深度卷积层 tf.keras.layers.DepthwiseConv2D。利用分组卷积和 1 乘 1 卷积的组合操作，可以构造相当于 Keras 中的二维深度可分离卷积层 tf.keras.layers.SeparableConv2D。
  • nn.Conv3d：普通三维卷积，常用于视频。参数个数 = 输入通道数×卷积核尺寸 (如 3 乘 3 乘 3)×卷积核个数 + 卷积核尺寸 (如 3 乘 3 乘 3) 。
  • nn.MaxPool1d : 一维最大池化。
  • nn.MaxPool2d：二维最大池化。一种下采样方式。没有需要训练的参数。
  • nn.MaxPool3d：三维最大池化。
  • nn.AdaptiveMaxPool2d：二维自适应最大池化。无论输入图像的尺寸如何变化，输出的图像尺寸是固定的。该函数的实现原理，大概是通过输入图像的尺寸和要得到的输出图像的尺寸来反向推算池化算子的 padding,stride 等参数。
  • nn.FractionalMaxPool2d：二维分数最大池化。普通最大池化通常输入尺寸是输出的整数倍。而分数最大池化则可以不必是整数。分数最大池化使用了一些随机采样策略，有一定的正则效果，可以用它来代替普通最大池化和 Dropout 层。
  • nn.AvgPool2d：二维平均池化。
  • nn.AdaptiveAvgPool2d：二维自适应平均池化。无论输入的维度如何变化，输出的维度是固定的。
  • nn.ConvTranspose2d：二维卷积转置层，俗称反卷积层。并非卷积的逆操作，但在卷积核相同的情况下，当其输入尺寸是卷积操作输出尺寸的情况下，卷积转置的输出尺寸恰好是卷积操作的输入尺寸。在语义分割中可用于上采样。
  • nn.Upsample：上采样层，操作效果和池化相反。可以通过 mode 参数控制上采样策略为 "nearest" 最邻近策略或 "linear" 线性插值策略。
  • nn.Unfold：滑动窗口提取层。其参数和卷积操作 nn.Conv2d 相同。实际上，卷积操作可以等价于 nn.Unfold 和 nn.Linear 以及 nn.Fold 的一个组合。其中 nn.Unfold 操作可以从输入中提取各个滑动窗口的数值矩阵，并将其压平成一维。利用 nn.Linear 将 nn.Unfold 的输出和卷积核做乘法后，再使用 nn.Fold 操作将结果转换成输出图片形状。
  • nn.Fold：逆滑动窗口提取层。

循环网络相关层​

  • nn.Embedding：嵌入层。一种比 Onehot 更加有效的对离散特征进行编码的方法。一般用于将输入中的单词映射为稠密向量。嵌入层的参数需要学习。
  • nn.LSTM：长短记忆循环网络层【支持多层】。最普遍使用的循环网络层。具有携带轨道，遗忘门，更新门，输出门。可以较为有效地缓解梯度消失问题，从而能够适用长期依赖问题。设置 bidirectional = True 时可以得到双向 LSTM。需要注意的时，默认的输入和输出形状是 (seq,batch,feature) , 如果需要将 batch 维度放在第 0 维，则要设置 batch_first 参数设置为 True。
  • nn.GRU：门控循环网络层【支持多层】。LSTM 的低配版，不具有携带轨道，参数数量少于 LSTM，训练速度更快。
  • nn.RNN：简单循环网络层【支持多层】。容易存在梯度消失，不能够适用长期依赖问题。一般较少使用。
  • nn.LSTMCell：长短记忆循环网络单元。和 nn.LSTM 在整个序列上迭代相比，它仅在序列上迭代一步。一般较少使用。
  • nn.GRUCell：门控循环网络单元。和 nn.GRU 在整个序列上迭代相比，它仅在序列上迭代一步。一般较少使用。
  • nn.RNNCell：简单循环网络单元。和 nn.RNN 在整个序列上迭代相比，它仅在序列上迭代一步。一般较少使用。

Transformer 相关层​

  • nn.Transformer：Transformer 网络结构。Transformer 网络结构是替代循环网络的一种结构，解决了循环网络难以并行，难以捕捉长期依赖的缺陷。它是目前 NLP 任务的主流模型的主要构成部分。Transformer 网络结构由 TransformerEncoder 编码器和 TransformerDecoder 解码器组成。编码器和解码器的核心是 MultiheadAttention 多头注意力层。

  • nn.TransformerEncoder：Transformer 编码器结构。由多个 nn.TransformerEncoderLayer 编码器层组成。

  • nn.TransformerDecoder：Transformer 解码器结构。由多个 nn.TransformerDecoderLayer 解码器层组成。

  • nn.TransformerEncoderLayer：Transformer 的编码器层。

  • nn.TransformerDecoderLayer：Transformer 的解码器层。

  • nn.MultiheadAttention：多头注意力层。

    Transformer参考文章

自定义模型层​

pytorch 不区分模型和模型层，都是通过继承 nn.Module 进行构建。我们只要继承 nn.Module 基类并实现 forward 方法即可自定义模型层。

示例：

import torch
from torch import nn
import torch.nn.functional as F

class Linear(nn.Module):
    __constants__ = ['in_features', 'out_features']

    def __init__(self, in_features, out_features, bias=True):
        super(Linear, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.weight = nn.Parameter(torch.Tensor(out_features, in_features))
        if bias:
            self.bias = nn.Parameter(torch.Tensor(out_features))
        else:
            self.register_parameter('bias', None)
        self.reset_parameters()

    def reset_parameters(self):
        nn.init.kaiming_uniform_(self.weight, a=math.sqrt(5))
        if self.bias is not None:
            fan_in, _ = nn.init._calculate_fan_in_and_fan_out(self.weight)
            bound = 1 / math.sqrt(fan_in)
            nn.init.uniform_(self.bias, -bound, bound)

    def forward(self, input):
        return F.linear(input, self.weight, self.bias)

    def extra_repr(self):
        return 'in_features={}, out_features={}, bias={}'.format(
            self.in_features, self.out_features, self.bias is not None
        )

损失函数

https://mp.weixin.qq.com/s/WSD5J48oKkZg24hQTmFtdQ

监督学习的目标函数由损失函数和正则化项组成。 (Objective = Loss + Regularization)

如果有需要，也可以自定义损失函数，自定义损失函数需要接收两个张量 y_pred，y_true 作为输入参数，并输出一个标量作为损失函数值。

常用的损失函数​

  • nn.MSELoss（均方误差损失，也叫做 L2 损失，用于回归）
  • nn.L1Loss（L1 损失，也叫做绝对值误差损失，用于回归）
  • nn.SmoothL1Loss (平滑 L1 损失，当输入在 -1 到 1 之间时，平滑为 L2 损失，用于回归)
  • nn.BCELoss (二元交叉熵，用于二分类，输入已经过 nn.Sigmoid 激活，对不平衡数据集可以用 weigths 参数调整类别权重)
  • nn.BCEWithLogitsLoss (二元交叉熵，用于二分类，输入未经过 nn.Sigmoid 激活)
  • nn.CrossEntropyLoss (交叉熵，用于多分类，要求 label 为稀疏编码，输入未经过 nn.Softmax 激活，对不平衡数据集可以用 weigths 参数调整类别权重)
  • nn.NLLLoss (负对数似然损失，用于多分类，要求 label 为稀疏编码，输入经过 nn.LogSoftmax 激活)
  • nn.CosineSimilarity (余弦相似度，可用于多分类)
  • nn.AdaptiveLogSoftmaxWithLoss (一种适合非常多类别且类别分布很不均衡的损失函数，会自适应地将多个小类别合成一个 cluster )

自定义损失函数​

自定义损失函数接收两个张量 y_pred,y_true 作为输入函数，并输出一个标量作为损失函数值。

也可以对 nn.Module 进行子类化，重写 forward 方法实现损失的计算逻辑，从而得到损失函数的类的实现。

下面是一个 Focal Loss 的自定义实现示范。Focal Loss 是一种对 binary_crossentropy 的改进损失函数形式。

它在样本不均衡和存在较多易分类的样本时相比 binary_crossentropy 具有明显的优势。

它有两个可调参数，alpha 参数和 gamma 参数。其中 alpha 参数主要用于衰减负样本的权重，gamma 参数主要用于衰减容易训练样本的权重。

从而让模型更加聚焦在正样本和困难样本上。这就是为什么这个损失函数叫做 Focal Loss。

示例：

class FocalLoss(nn.Module):
    
    def __init__(self,gamma=2.0,alpha=0.75):
        super().__init__()
        self.gamma = gamma
        self.alpha = alpha

    def forward(self,y_pred,y_true):
        bce = torch.nn.BCELoss(reduction = "none")(y_pred,y_true)
        p_t = (y_true * y_pred) + ((1 - y_true) * (1 - y_pred))
        alpha_factor = y_true * self.alpha + (1 - y_true) * (1 - self.alpha)
        modulating_factor = torch.pow(1.0 - p_t, self.gamma)
        loss = torch.mean(alpha_factor * modulating_factor * bce)
        return loss

神经网络的结构设计

  1. 高低融合（将高层次特征宇低层次特征融合，提升特征维度的丰富性和多样性，像人一样同时考虑整体和细节）

    DeepWide,UNet，特征金字塔 FPN...

  2. 权值共享（一个权值矩阵参与多个不同的计算，降低参数规模并同时缓解样本稀疏性，像人一样一条知识多处运用）

    CNN,RNN,FM...

  3. 动态适应（不同的输入样本使用不同的权值矩阵，动态地进行特征选择并赋予特征重要解释性，像人一样聚焦重要信息排除干扰信息）

    各种 Attention 机制...

    SENet 原理 https://zhuanlan.zhihu.com/p/65459972

DIN 深度兴趣网络

DIN 论文

Attention 机制简单总结

DIN+DIEN

Attention 机制的一些常用功能和典型范例总结如下：

  1. 动态特征选择，根据样本不同动态地赋予特征以不同的权重，典型范例如 SENet 中的 SEAttention，DIN 中的 Attention .

  2. 动态特征交互，动态地构建特征之间的交互强弱关系，提取高阶特征。典型范例如 Transformer 中的的 Attention。

  3. 动态模块集成，类似多模型融合集成，但是不同子模块的权重是动态的。典型范例如 MOE 中的门控注意力机制。

在 attention 场景中，输入分成 Query（Q）和 Key（K）

Query 是当前关注项的 Embedding 向量，

Key 是待和当前关注项进行匹配地 Embedding 向量

例如在广告 CTR 领域，Query 就是当前待预估的广告，Key 就是用户历史上点击过的广告，通过 Attention 机制建立当前待预估的广告和用户历史上点击过的广告的相关性强弱。

Attention 机制的核心实现是计算注意力权重，一些的常用实现形式如下：

attention=f(Q,K)

1，多层感知机方法

先将 Query 和 Key 进行拼接，然后接一个多层感知机。

这种方法不需要 Query 和 Key 的向量长度相等，Query 和 Key 之间的交互方式是通过学习获得的。

f(Q,K)=mlp([Q;K])f(Q,K)=mlp([Q;K])

2,Bilinear 方法

通过一个权重矩阵直接建立 Query 和 Key 的关系映射，计算速度较快，但是需要 Query 和 Key 的向量长度相同。

f(Q,K)=QWKTf(Q,K)=QWK^T

3,Scaled-Dot Product

这种方式直接求 Query 和 Key 的内积相似度，没有需要学习的参数，计算速度极快，需要 Query 和 Key 的向量长度相同。考虑到随着向量维度的增加，最后得到的权重也会增加，对其进行 scaling。

DIEN 深度兴趣演化网络

最近的行为可能比较远的行为更为重要，可以用循环神经网络 GRU 建立随时间的演化的模型

DIEN 论文

https://mp.weixin.qq.com/s/zNZ5GxwrylY-suXitE40Og

  • 一是引入 GRU 来从用户行为日志序列中自然地抽取每个行为日志对应的用户兴趣表示 (兴趣抽取层)。
  • 二是设计了一个辅助 loss 层，通过做一个辅助任务 (区分真实的用户历史点击行为和负采样的非用户点击行为) 来强化用户兴趣表示的学习。
  • 三是将注意力机制和 GRU 结构结合起来 (AUGRU: Attention UPdate GRU) ，来建模用户兴趣的时间演化得到最终的用户表示 (兴趣演化层)。

a

1. 兴趣抽取层​

图中的 b(t)b(t) 是用户的行为序列，而 e(t)e(t) 是对应的 embedding。随着自然发生的顺序， e(t)e(t) 被输入 GRU 中，这就是兴趣抽取层。

也是 DIEN 的第一条创新：引入 GRU 来从用户行为日志序列中自然地抽取每个行为日志对应的用户兴趣表示 (兴趣抽取层)。

##2. 辅助 loss

如果忽略上面的 AUGRU 环节，GRU 中的隐状态 h(t)h(t) 就应该成为用户的行为序列最后的表示。

如果直接就这样做，也不是不可以，但是学习到的东西可能不是我们想要的用户兴趣表示，或者说 h(t)h(t) 很难学习到有意义的信息。

因为 h(t)h(t) 的迭代经过了很多步，然后还要和其他特征做拼接，然后还要经过 MLP，最后才得到输出去计算 Loss。

这样的结果就是最后来了一个正样本或负样本，反向传播很难归因到h(t)h(t) 上。

基于此 DIEN 给出了第二个要点：使用辅助 Loss 来强化 h(t)h(t) 的学习。

辅助 Loss :这里设计了一个辅助任务，使用 h(t)h(t) 来区分真实的用户历史点击行为和负采样的非用户点击行为。

由于 h(t)h(t) 代表着 t 时刻的用户兴趣表示，我们可以用它来预测 t+1 时刻的广告用户是否点击。

因为用户行为日志中都是用户点击过的广告 (正样本，e(t)e(t) )，所以我们可以从全部的广告中给用户采样同样数量的用户没有点击过的广告作为负样本 e′(t)e^{'}(t) 。

结合 h(t)h(t) 和 e(t)e(t) , e′(t)e^{'}(t) 作为输入，我们可以做一个二分类的辅助任务。

这个辅助任务给 h(t)h(t) 在每个 t 时刻都提供了一个监督信号，使得 h(t)h(t) 能够更好地成为用户兴趣的抽取表示。

真实应用场合下，你把开始的输入和最后的要求告诉网络，它就能给你一个好的结果的情况非常少。

大多数时候是需要你去控制每一步的输入输出，每一步的 loss 才能防止网络各种偷懒作弊。

辅助 loss 能够使得网络更受控制，向我们需要的方向发展，非常建议大家在实际业务中多试试辅助 loss。

3. 兴趣演化层​

通过兴趣抽取层和辅助 loss，我们得到了每个 t 时刻用户的一般兴趣表示。

注意这个兴趣表示是一般性的，还没有和我们的候选广告做 Attention 关联。

在 DIN 中，我们通过 Attention 机制构建了和候选广告相关的用户兴趣表示。

而在 DIEN 中，我们希望建立的是和和候选广告相关，并且和时间演化相关的用户兴趣表示。

DIEN 通过结合 Attention 机制和 GRU 结构来做到这一点，这就是第三点创新 AUGRU : Attention UPdate Gate GRU。

RNN 序列模型层（SimpleRNN，GRU，LSTM 等）可以用函数表示如下：

ht=f(h(t−1),it)h_t=f(h_{(t-1)},i_t)

这个公式的含义是：t 时刻循环神经网络的输出向量 hth_t 由 t-1 时刻的输出向量 ht−1h_{t-1} 和 t 时刻的输入 iti_t 变换而来。

为了结合 Attention 机制和 GRU 结构，我们需要设计这样的一个有三种输入的序列模型。

ht=g(h(t1),it,at)h_t=g(h_{(t_1)},i_t,a_t)

这里的 ata_t 是** t 时刻的用户兴趣表示输入 iti_t 和候选广告计算出的 attention 得分**，是个标量。

GRU 的具体函数形式：

ut=σ(Wuit+Uuhh−1+bu)    (1)rt=σ(Writ+Urhh−1+br)    (2)nt=tanh(Wnit+rt∘Unht−1+bn)    (3)ht=ht−1−ut∘ht−1+ut∘nt    (4)u_t=\sigma(W^ui_t+U^uh_{h-1}+b^u) \ \ \ \ (1) \\ r_t=\sigma(W^ri_t+U^rh_{h-1}+b^r) \ \ \ \ (2) \\ n_t=tanh(W^ni_t+r_t\circ U^nh_{t-1}+b^n) \ \ \ \ (3) \\ h_t=h_{t-1}-u_t \circ h_{t-1}+u_t \circ n_t \ \ \ \ (4)

∘\circ 表示哈达玛积，也就是两个向量逐位相乘。

其中（1）式和（2）式计算的是更新门 utu_t 和 重置门 rtr_t ,是两个长度和 hth_t 相同的向量。

更新门用控制每一步 hth_t 被更新的比例，更新门越大，hth_t 更新幅度越大。

重置门用于控制更新候选向量 ntn_t 中前一步的状态 ht−1h_{t-1} 被重新放入的比例，重置门越大，更新候选向量中 ht−1h_{t-1} 被重新放进来的比例越大。

注意到 (4) 式 实际上和 ResNet 的残差结构是相似的，都是 f(x) = x + g(x) 的形式，可以有效地防止长序列学习反向传播过程中梯度消失问题。

如何在 GRU 的基础上把 attention 得分融入进来呢：

  • 用 ata_t 缩放输入 iti_t , 这就是 AIGRU: Attention Input GRU。其含义是相关性高的在输入端进行放大。

    这里的 ata_t 是t 时刻的用户兴趣表示输入 iti_t 和候选广告计算出的 attention 得分，是个标量。

    AIGRU 实际上并没有改变 GRU 的结构，只是改变了其输入，这种方式对 Attention 的使用比较含蓄。

  • 用 ata_t 代替 GRU 的更新门，这就是 AGRU: Attention based GRU。其含义是用直接用相关性作为更新幅度。

    AGRU 是改变了 GRU 的结构的，并且对 Attention 的使用非常激进，完全删掉了 GRU 原有的的更新门。

  • 用 ata_t 缩放 GRU 的更新门 utu_t ，这就是 AUGRU: Attention Update Gate GRU。其含义是用用相关性缩放更新幅度。

    AUGRU 也是改变了 GRU 的结构的，并且对 Attention 的使用比较折衷，让 Attention 缩放 GRU 原有的更新幅度。

informer 模型

与 transformer 类似，为一种专为 LSTD（长序列时间序列预测）设计的基于 transformer 的改进模型 informer，来解决 transformer 在应用于 LSTF 存在的一些严重的问题。比如二次时间复杂度、较高的内存使用量和编解码器结构的固有限制等。

informer 模型的三个特点

  1. 采用 ProbSparse 注意力机制
  2. 自注意力提炼、
  3. 生成器解码器。提出生成式的 decoder 机制，在预测序列（也包括 inference 阶段）时进一步得到结果，而不是 step-by-step。直接将预测时间复杂度由 O（n）降到 O（1）

论文：https://arxiv.org/abs/2012.07436

a

资料​

代码解读

知识继承 knowledge distillation

利用大模型去指导小模型

可以利用 DGMR 模型去指导小模型

这样可以达到小模型也会有接近 DGMR 模型的性能。

https://gitee.com/linziyang233/imgs/raw/master/img/23ac7847b88bb728e6273bcc43adfad.png

dm

【视频 16:00 处】https://www.bilibili.com/video/BV1Wv411h7kN?p=52&vd_source=14431a1e124792205879efa3a5444ef3

VAE-GAN

B 站 李宏毅 视频

自编码器 (Auto-encoder) (上)

VAE​

  1. encoder 的作用是编码，也就是将输入的图片 image1 转换成一个向量 vector

  2. decoder 的作用是解码，也就是将向量 vector 转换图片 image2

    其中，image1 和 image2 要尽量相同，原因是我们希望对同一个东西进行编解码后的产物仍然是自己。

GAN​

  1. generator：就是 VAE 的 decoder，将向量 vector 转换为 image
  2. discriminator：评判 generator 产生的 image 是 real 还是 fake，给出一个 scalar（分数或者可能性，或者二分类结果）

VAE-GAN

运作流程​

  1. 初始化 encoder、decoder、discriminator（三个神经网络）

  2. 迭代更新

    • 从 database 中随机采样，x1，x2 ... xM
    • x1，x2 ... xM 输入到 encoder 中 产生 z =En（x）
    • 将 z1，z2 ... zM 输入到 decoder 中 产生 x=De（z）
    • 从某个分布（均匀分布，高斯分布等）取样 z1，z2，zm
    • 将 z1，z2，zm 输入到 decoder 产生 x=De（z）

    encoder 和 decoder 合起来的目标是：一张图片编解码之后尽量保持原样。因此， encoder 的更新准则是：编解码前后图片的方差尽可能小；编码前图片的分布和解码后图片的分布尽可能一致（分布用 KL 散度描述）； decoder 的更新准则是：编解码前后图片的方差尽可能小；解码后的图片得分尽量高，reconstructed 产生的图片的得分也尽量高 discriminator 的更新准则是：要尽量能区分 generator，reconstructed 和 realistic 的图片；因此对于原始图像的得分要尽量高，对于 generator，reconstructed 的图片的得分要尽量低。 注意：上面的图片有三种情况：1）原始图片（分布在 database 中，realistic）2）原始图片经过编解码之后产生的图片（generator）3）从某个分布中随机采样得到 z，输入解码器中获得的图片（reconstructed）