VAE

变分自编码器（Variational AutoEncoder，VAE）是一种深度生成模型，其思想是利用神经网络来分别建模两个复杂的条件概率密度函数。

（1）用神经网络来估计变分分布 $q(z;\phi)$ ,称为推断网络。理论上 $q(z;\phi)$ 可以不依赖 x，但由于 $q(z;\phi)$ 的目标是近似后验分布 $p(z|x;\theta)$ ,其和 x 相关，因此变分密度函数一般写为 $q(z|x;\phi)$ 。推断网络的输入为 x。输出为 x，输出为变分分布 $q(z|x;\phi)$ .

（2）用神经网络来估计概率分布 $p(x|z;\theta)$ ，称为生成网络 。生成网络的输入为 z，输出的概率分布为 $p(x|z;\theta)$

将推断网络和生成网络合并就得到了变分自编码器的整个网络结构，如

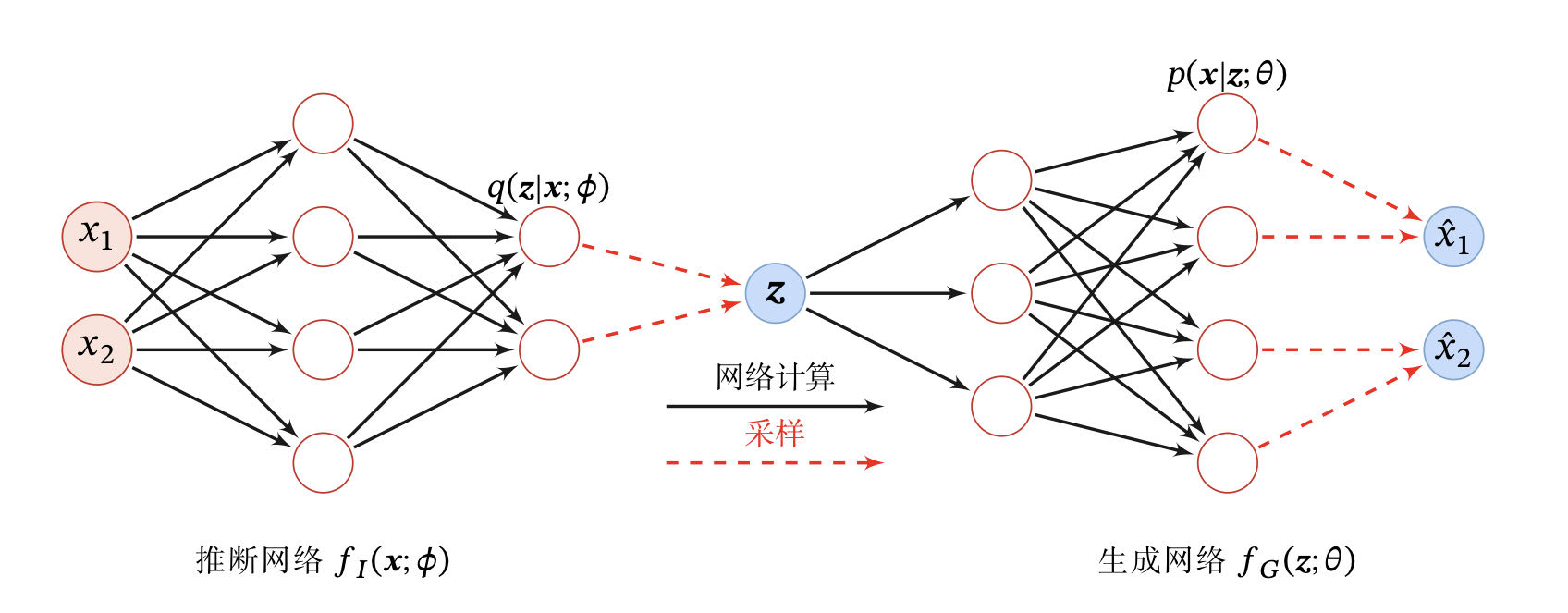
变分自编码器的网络结构

变分自编码器的名称来自于整个网络结构和自编码器比较类似。推断网络看作是“编码器”，将可观测变量映射为隐变量。生成网络可以看作是“解码器”，将隐变量映射为可观测变量。但变分自编码器背后的原理和自编码器完全不同。变分自编码器中的编码器和解码器的输出为分布（分布的参数）而不是确定的编码。

推断网络

假设 $q(z|x;\phi)$ 是服从对角化协方差的高斯分布，

$$q(z|x;\phi) =N(z;\mu_I,\sigma^2_II)$$

$其中 \ \ \mu_I\ \ 和\ \ \sigma^2_I \ \ 是高斯分布的均值和方差，可以通过推断网络\ \ f_I(x;\phi)\ \ 来预测$

$$\begin{bmatrix} \mu_I \\ \sigma^2_I \end{bmatrix} =f_I(x;\phi)$$

$其中推断网络\ \ f_I(x;\phi) \ \ 可以是一般的全连接网络或卷积网络，比如一个两层的神经网络$ .

推断网络的目标

推断网络的目标是使得 $q(z|x;\phi)$ 尽可能的接近真实的后验 $p(z|x;\theta)$ ，需要找到一组网络参数$\phi^*$ 来最小化两个分布的 KL 散度，即

$$\phi^*\underset{\phi}{argmin}KL(q(z|x;\phi),p(z|x;\theta))$$

然而直接计算上面的 KL 散度是不可能的，因为 $p(z|x;\theta)$ 一般无法计算。传统方法是利用采样或者变分法来近似推断。变分推断是用简单的分布 q 去近似复杂的分布 $q(z|x;\theta)$ ,但是，在深度生成模型中，$p(z|x;\theta)$ 通常比较复杂，很难用简单的分布去近似。 但可以通过转换，使推断网络的目标函数可以转换为

$$\phi^* =\underset{\phi}{argmin}ELBO(q,x;\theta,\phi)$$

即推断网络的目标函数转换为寻找一组网络参数 $\phi^*$ 使得证据下界 $ELBO(q,x;\theta,\phi)$ 最大，这和变分推断的转换类似。

生成网络

生成模型的联合分布 $p(x,z;\theta)$ 可以 分为两部分：隐变量 z 的先验分布 $p(z;\theta)$ 和条件概率分布$p(x|z;\theta)$ 先验分布 $p(x|z;\theta)$ 为简单起见，我们一般假设隐变量 z 的先验分布为各向同性的标准高斯分布 $N(z|0,I)$ ,隐变量 z 的每一维都是独立的。 条件概率分布 $p(x|z,\theta)$ 条件概率分布 $p(x|z;\theta)$ 可以通过生成网络来建模。为简单起见，我们同样用参数化的分布族来表示条件概率分布 $p(x|z;\theta)$ ,这些分布族的参数可以用生成网络计算得到。

生成网络的目标

生成网络 $f_G(z;\theta)$ 的目标是找到一组网络参数 $\theta^*$ 来最大化 $ELBO(q,x;\theta,\phi)$

$$\theta^* =\underset{\theta}{argmin}ELBO(q,x;\theta,\phi)$$